1. Overview
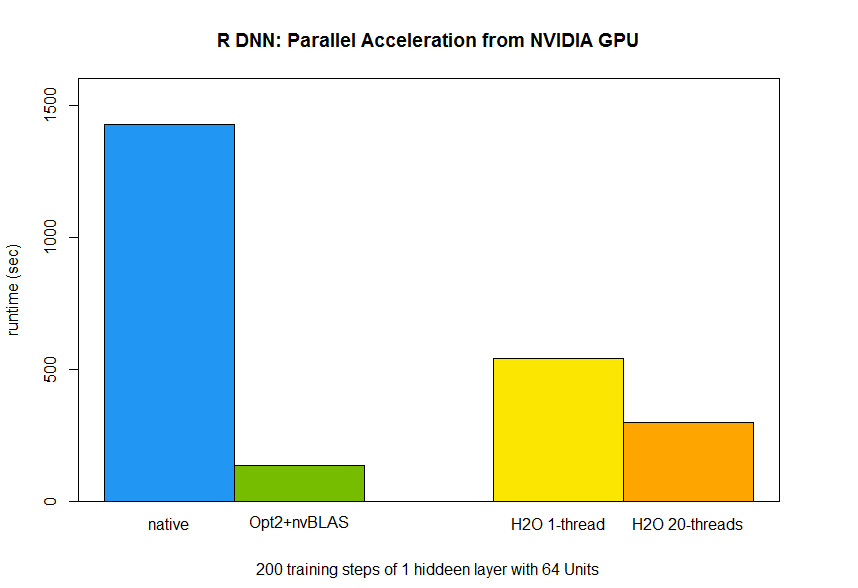
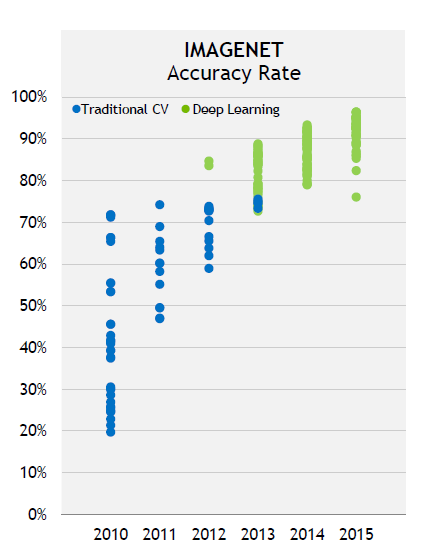
In the previous post (here), we have analyzed the performance gain of R in the heterogeneous system by accelerators, including NVIDIA GPU and Intel Xeon Phi. Furthermore, GPU accelerated packages can greatly improve the performance of R. Figure 1 shows the download statistics of CRAN over the years. Obviously, GPU is more and more recognized by the R community. 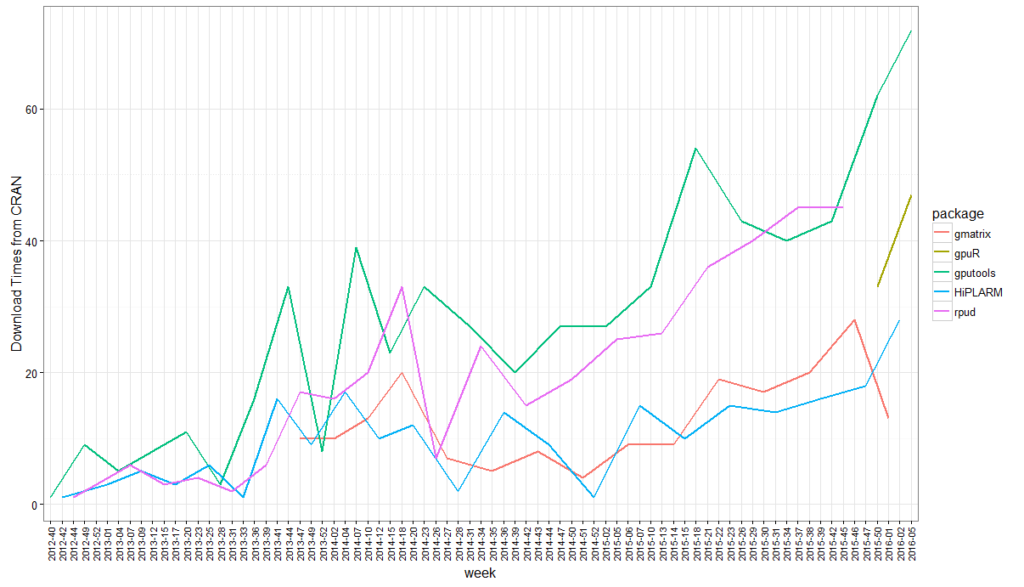
Figure 1 Download statistics of CRAN Package applied to the GPGPU environment over the years
2. GPU-accelerated packages
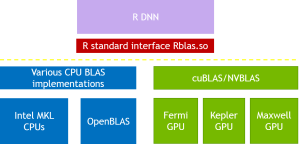
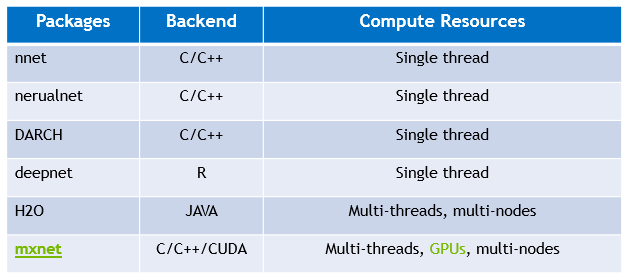
Matrix operation (BLAS) is one of the most important operations in data analysis, such as co-matrices in recommended systems and convolution calculations in deep learning. The matrix and the vector multiplication and other standard operations in R can be accelerated by GPU significantly. The most simple way to use GPU in R is through the nvBLAS (cuBLAS) library provided by NVIDIA, but other GPU accelerated packages (gputools, gmatrix, gpuR) provides a richer software and hardware interface, as shown in Table 1.
Table 1 Function comparison of the R package supported for GPGPU

2.1 Data type
Double-precision (DP) is used in nvBLAS and gputools to align with the default double precision mode of R. On the other hand, gmatrix and GPU can be more flexible for the user to choice single-precision (SP) or double-precision (DP) in the computations. And even gmatrix can support integer matrix computing. The SP computation mode can significant leverage the capability in low-mid level NVIDIA GPU cards, such as Tesla M40 and Geforce series GPUs, where the main computing power from SP floating-point operations. Therefore, this is a good news common desktop GPU users.
2.2 Data transfer
When using the GPU as a coprocessor to speed up the application, the cost of data transfer usually takes a significant portion of the time, and the size of the GPU’s built-in memory will also limit whether the application can be executed. One of the main advantages of nvBLAS is that it supports block-based data copy and calculations between CPU and GPU, so the memory required from R code can be large than built-in GPU memory. However, the host-to-device memory copy, the calculation, and the final device-to-host results are performed in a synchronized mode so that the user cannot isolate the data transfer and calculation in nvBLAS. gmatrix and gpuR provide the asynchronous mode of communication and calculation, the user can separate the data copy and the real calculation. For example, gpuR provided in the vcl * series API, it will return in the R console immediately and then R will execute the next CPU command, while GPU is computing. In this way, both CPU and GPU are working simultaneously. And we can get much more performance boost.
2.3 Programming model
Frist, nvBLAS, gmatrix are based on the CUDA programming model and it will show better performance in NVIDIA series of GPUs but the shortage is poor portability. Then, gpuR is based on OpenCL, a standard heterogeneous programming interface, and more flexible. The user program of OpenCL can be executed on much more platforms, such as CPU, GPGPU, Intel Xeon Phi and FPGA.
3. Performance Benchmark and Analysis
3.1 Test environment
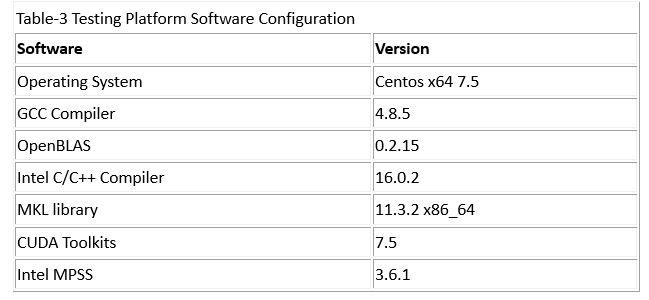
The test is performed on the Ali cloud HPC platform: G2 server with NVIDIA Tesla K40m, G4 server with Tesla M40. Ali cloud HPC provides independent physical server + GPU accelerator card without virtualization overhead for computing-intensive applications. Regarding GPU equipment, K40m is designed with Kepler architecture while M40 with Maxwell architecture. The M40 targets for deep learning markets especially for training. Its SP floating-point peak performance reaches 7TFlops, but DP is only 0.2TFlops.
Table 2 Ali cloud hardware platform configuration
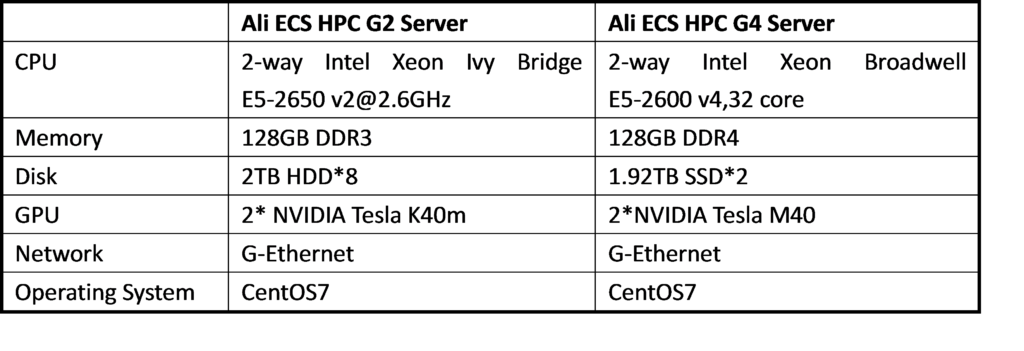
Table 3 List of M40 and K40m hardware parameters

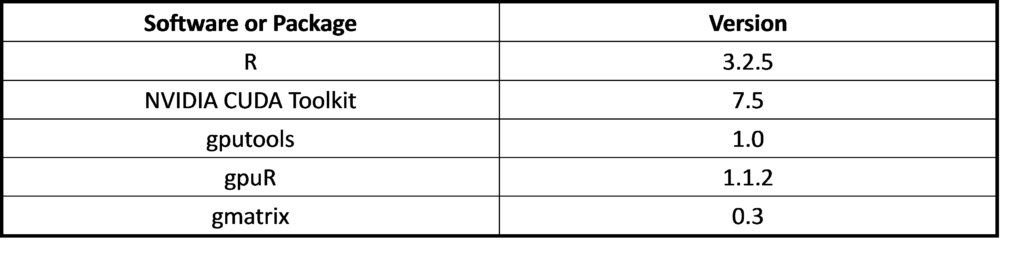
Table 4 Software of test used
3.2 Performance Analysis on K40 for double precision
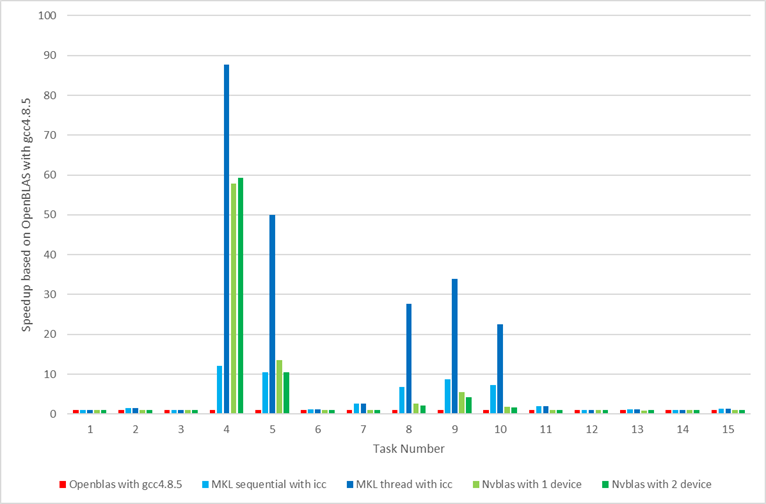
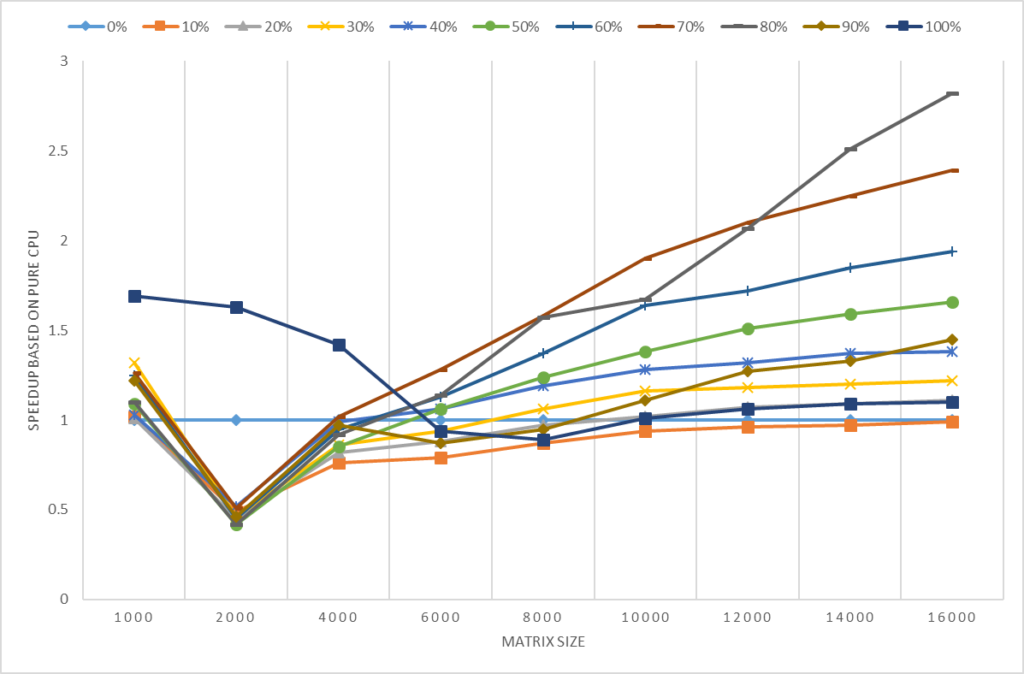
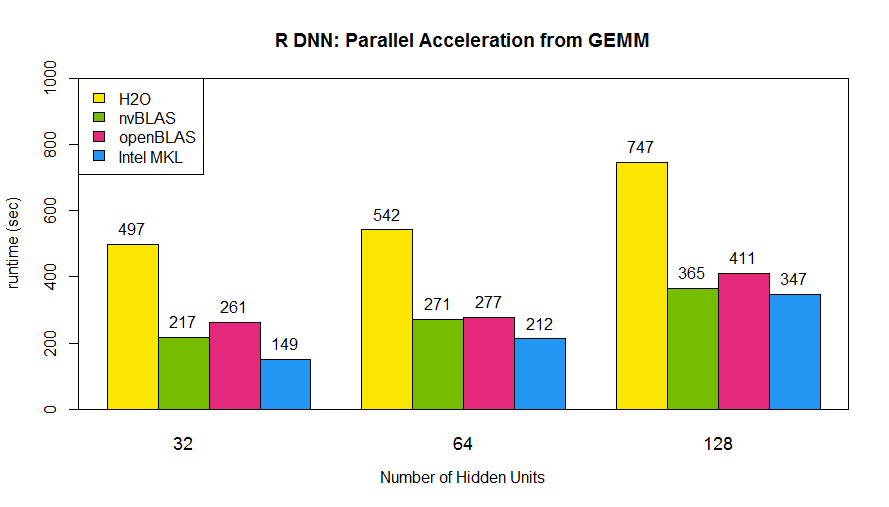
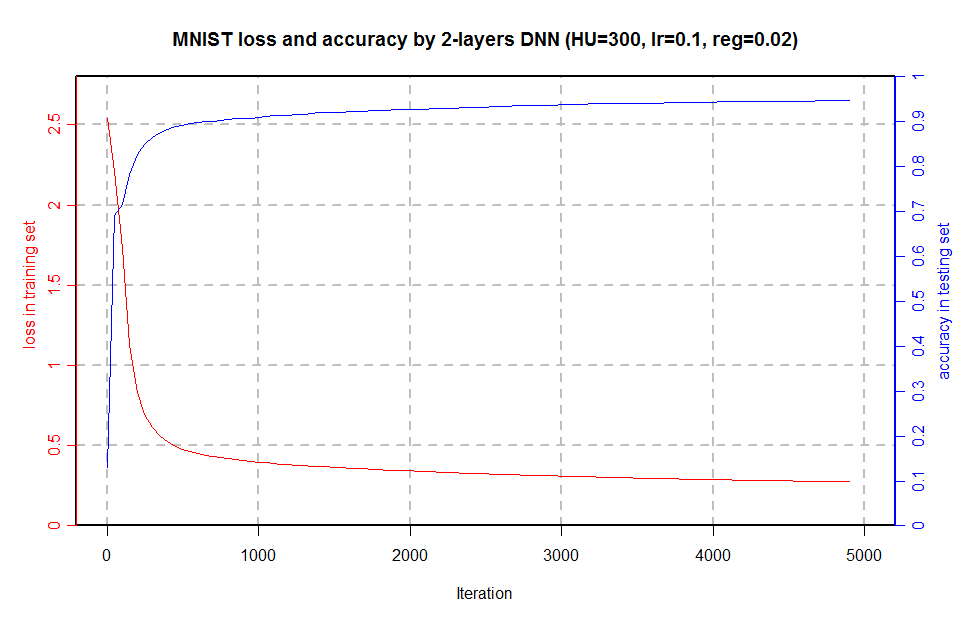
First, let’s compare the double-precision performance of each package on the Tesla series. We use nvblas performance as the baseline and compare the calculation time of three different sizes of matrix multiplications. In the testing code as below, we only counted the execution time of core API (% %, gemm, gpuMatMult) following depth analysis. \R code for gpuR, gmatrix, gputools and nvblas with DP calculation mode
1 | library(gpuR) |
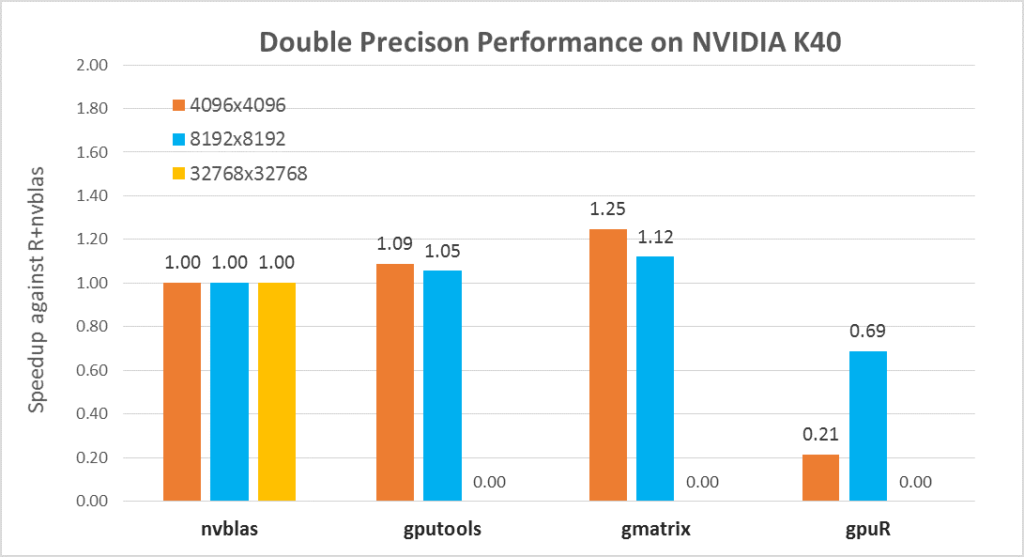
Figure 2 Performance of the software package with the size change
In general, nvblas, gputools and gmatrix show very similar performance, because they use cuBLAS as the backend. gpuR’s performance is relatively low and variety with input sizes, such as the 4096 matrix only achieves 20% of nvblas performance but 8192 matrices can reach ~70%. From computation pattern, gputools and gmatrix apply dgemm_sm_heavy_ldg_nn API interfaces of cuBLAS to complete the matrix calculations, and computational efficiency will be slightly higher than nvblas of the block matrix calculation mode. From memory usage, as Figure 2, nvblas is the only one able to complete the large memory (out of cores/memory) calculation. For the largest matrix 32768, GPU packages (gputools, gmatrix, gpuR) will throw an exception of memory overflow. More details In Table 5, input matrix are divided into many small pieces, and then are transmitted to the GPU for computations by nvblas.
Table 5. Analysis of memory copy times from nvprof
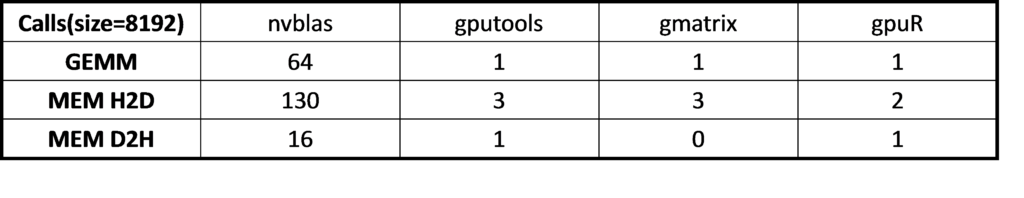 For gmatrix, matrix (A, B, C for C = A*B) are copied to GPU and C matrix stored in the GPU side after the calculation, involving three times host-to-device data transfer and without device-to-host transfer. For gputools matrix (A, B) are copied to GPU, the result matrix ( C ) is copied back to the host side so totally twice host-to-device and once device-to-host data transfer. Because the host-to-device data transfer is faster than device-to-host, gmatrix could get better performance than gputools as table 6 shown. Finally, we take a look at gpuR performance. The matrix calculation leverages OpenCL API that the performance is less optimized on NVIDIA GPU in table 6. GEMM compute kernel _prod_TT is much slower than gputools and gmatrix. Take 8192 for example, the calculation time of cublas API is 911.4 ms and 912.3 ms for gputools and gmatrix while OpenCL is 2172.5 ms for gpuR.
For gmatrix, matrix (A, B, C for C = A*B) are copied to GPU and C matrix stored in the GPU side after the calculation, involving three times host-to-device data transfer and without device-to-host transfer. For gputools matrix (A, B) are copied to GPU, the result matrix ( C ) is copied back to the host side so totally twice host-to-device and once device-to-host data transfer. Because the host-to-device data transfer is faster than device-to-host, gmatrix could get better performance than gputools as table 6 shown. Finally, we take a look at gpuR performance. The matrix calculation leverages OpenCL API that the performance is less optimized on NVIDIA GPU in table 6. GEMM compute kernel _prod_TT is much slower than gputools and gmatrix. Take 8192 for example, the calculation time of cublas API is 911.4 ms and 912.3 ms for gputools and gmatrix while OpenCL is 2172.5 ms for gpuR.
Table 6 Time overhead on GPU side at matrix size of 8192 * 8192
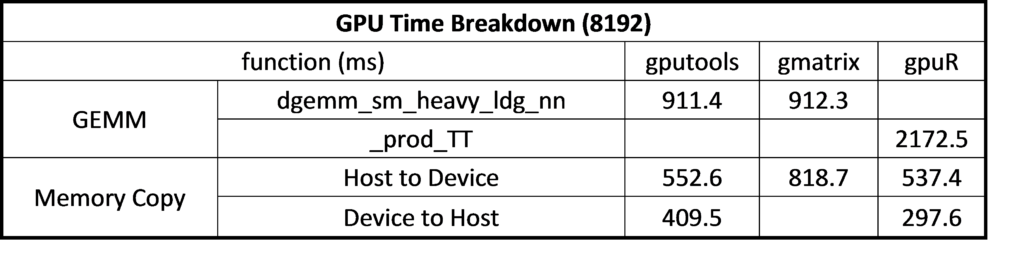
3.3 Performance Analysis on M40 for single precision
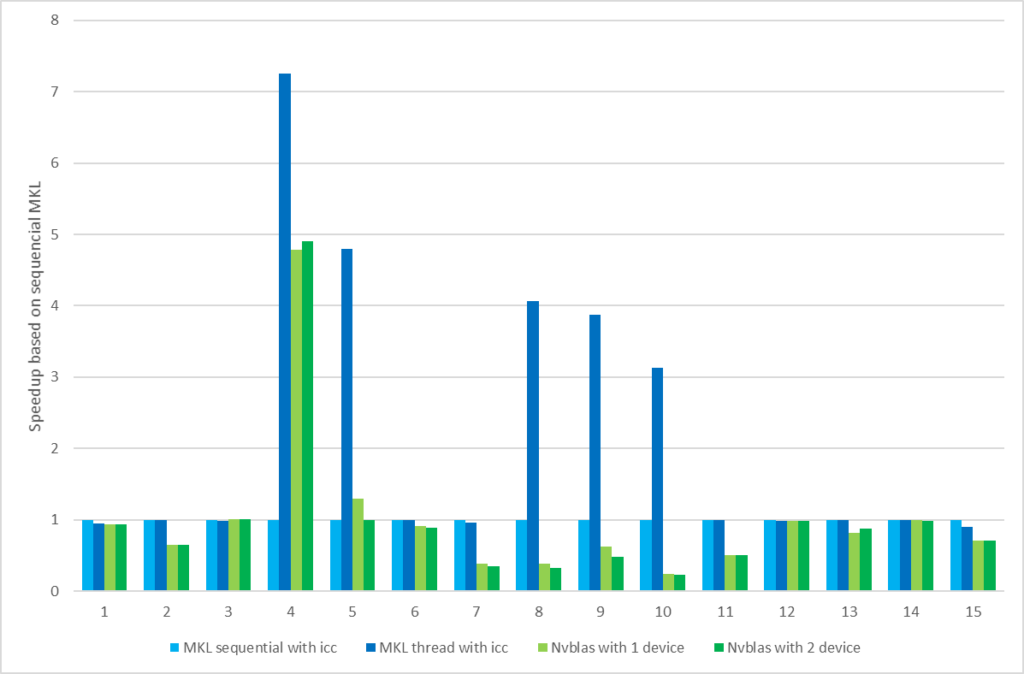
Single precision is quite important for data scientists but openBLAS, nvblas, and gputools use default double-precision (DP) calculation mode of R. So, it will lack competition in some hardware such as Tesla M40 where the DP performance is only 0.2T. In this parts, we will show you how to leverage SP performance in R by gmatrix and gpuR. In the blow testing, we take openBLAS performance results as the baseline. *R code of gmatrix and gpuR with SP calculation mode
1 | library(gpuR) |
In Figure 3, gmatrix and gpuR with SP calculation model show a very good performance boost. For the 4096 matrix size, gmatrix is 18X faster than openBLAS and 37X faster (18.22 / 0.51) than nvblas. 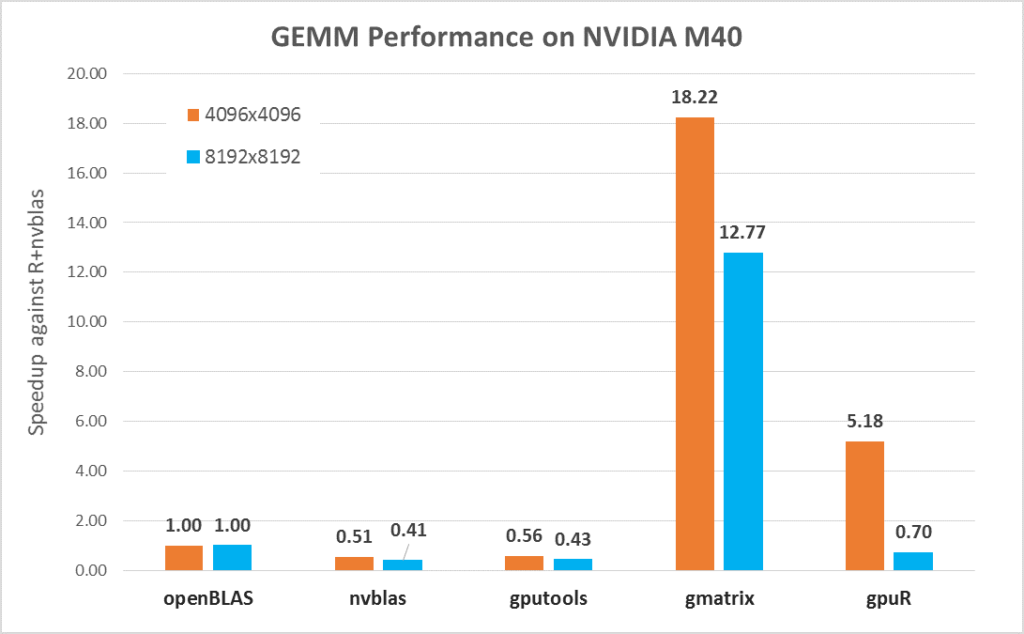
Figure 3 Performance with SP mode on M40
More details in Table 7, it is obvious that the computation time of SP is much less than the calculation time of DP. The calculation time of DP is about 6000 ms (nvblas, gputools), while the calculation time of SP is only about 200 ms (gmatrix) and 500 ms (gpuR). From the memory point of view, gpuR on CPU uses SP data type and gmatrix on CPU is still DP. From Table 7, we can see that memory transfer time of gputools and gmatrix is almost same, and gpuR memory transfer time is only half of it (gmatrix 153.4 ms .vs. gpuR 77.7 ms). So, gpuR are more efficient in memory usage for SP and will good for the small size of computations. Note, gmatrix does not use MEM D2H by default. In order to compare memory transfer performance with other packages, H (C) is added into the source code to make a consistent comparison.
Table 7 SP/DP performance of each Package on the M40 with matrix size of 8192*8192
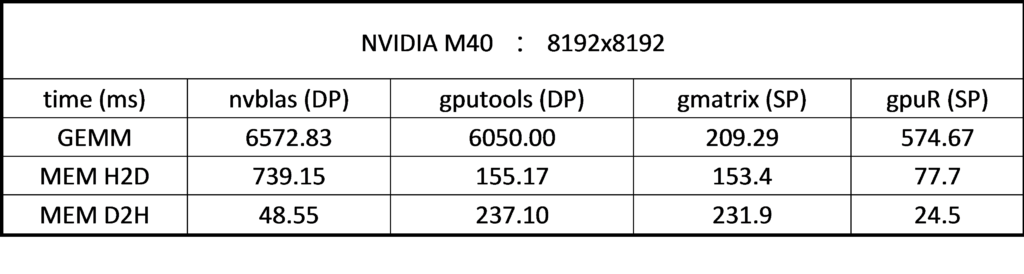
Note: GEMM kernel API on M40 is magma_lds128_dgemm_kernel.
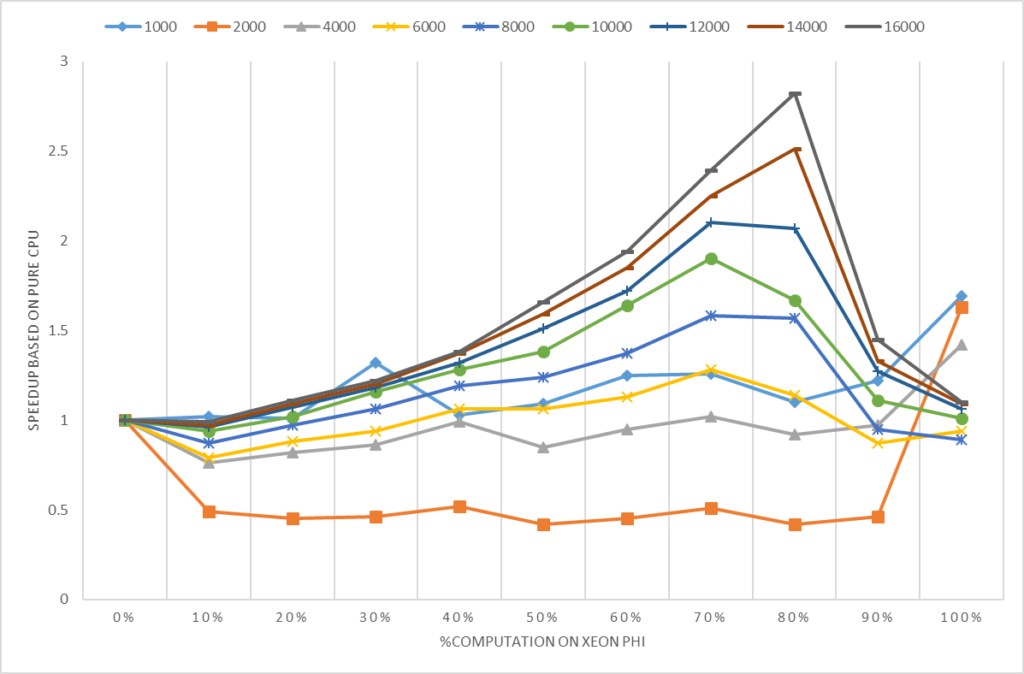
3.4 Asynchronous Mode
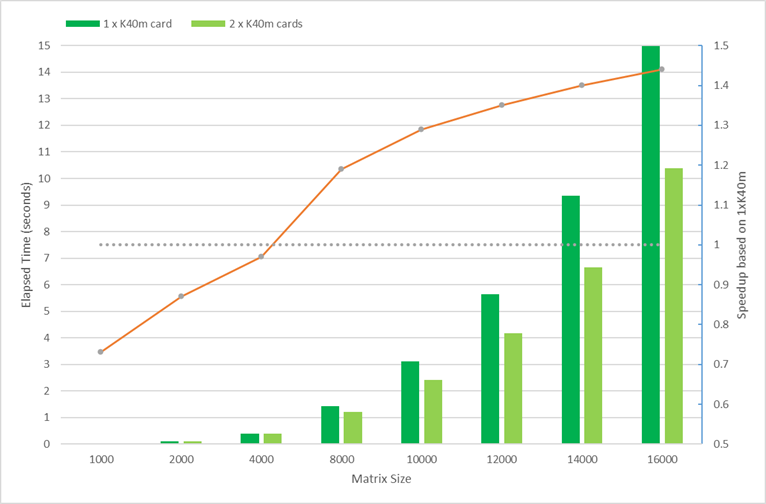
For the advanced user, gpuR provides a set of asynchronous mode interface. By using asynchronous interfaces, the R program will immediately return to the CPU program side after calling the interface of vcl *, and the user can continue to perform other tasks on the CPU. When the user explicitly accesses and use vcl * data, if the calculation has not yet completed, R will continue to wait; if the calculation has been completed, users can directly use. Therefore, users can use concurrency of CPU and GPU to hide the communication and computing time on GPU. In Figure 4, we compared the computing time between gpuR in asynchronous mode and gmatrix in synchronous mode (gmatrix shows the best performance in synchronous mode testing). As figure 4 shown, the sync-API execution time increases as the computational task increases but async-API keep a very tiny cost for all input size because the async-API do not include any actual calculations and just returns immediately. So, in the best case, we can hide all GPU execution time with CPU computation with a very tiny overhead. *gpuR running code with SP in asynchronous mode
1 | library(gpuR) |
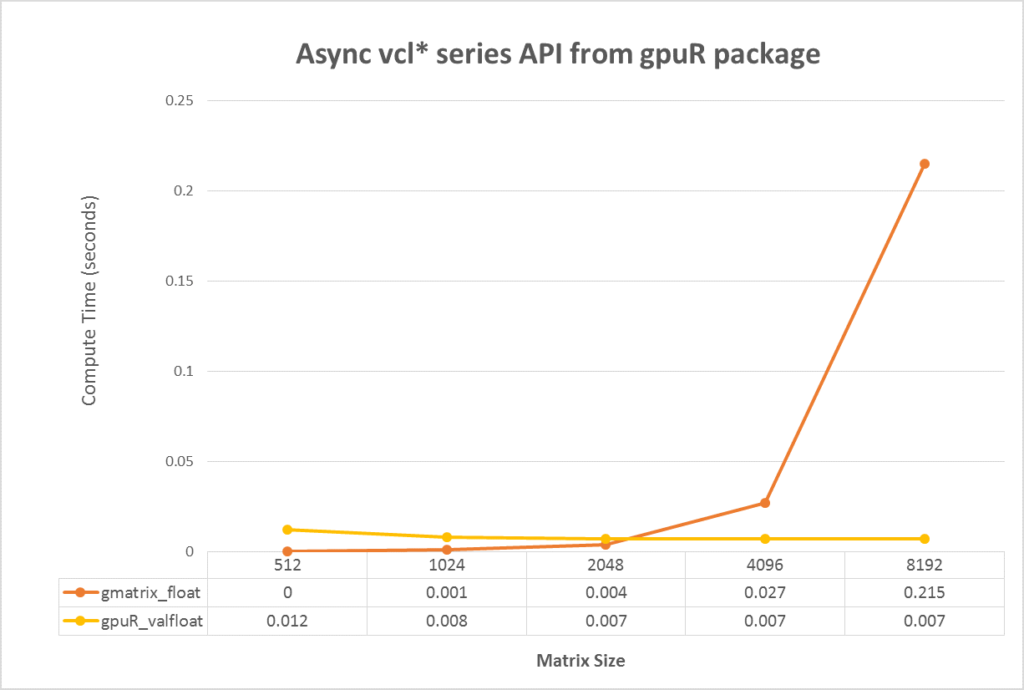
Figure 4. Performance comparison between gpuR in asynchronous mode and gmatrix in synchronization mode
4. Conclusions and recommendations
In this blog, we analyze the performance of the most popular GPU computing package. Each package has its own unique, but also have their own advantages and disadvantages. In practices, we need to choose according to specific needs. Based on the calculation platform, the calculation mode and the ease of use, it is recommended as follows:
- nvblas is suitable for
- NVIDIA GPU card
- Double precision calculation
- Large memory consumption of the calculation, nvblas provides a very good performance and scalability
- Beginners
- gputools is suitable for
- NVIDIA GPU card
- Double precision calculation
- Easy to use, and same API interface with R
- Beginners
- gmatrix is suitable for
- NVIDIA GPU card
- Single/Double precision calculation
- Multilevel BLAS interface(level 1,2,3)
- More extension in GPU (colsum, sort)
- Memory transfer optimization but the user needs to know where the memory is saved
- Intermediate/Senior users or R developers
- gpuR is suitable for
- Single/Double precision calculation
- Multilevel BLAS interface(level 1,2,3)
- Heterogeneous systems work on most of the platforms such as AMD, Intel Xeon Phi, Intel GPUs
- Asynchronous calculation mode, you can better hide the communication time
- Intermediate/Senior users or R developers
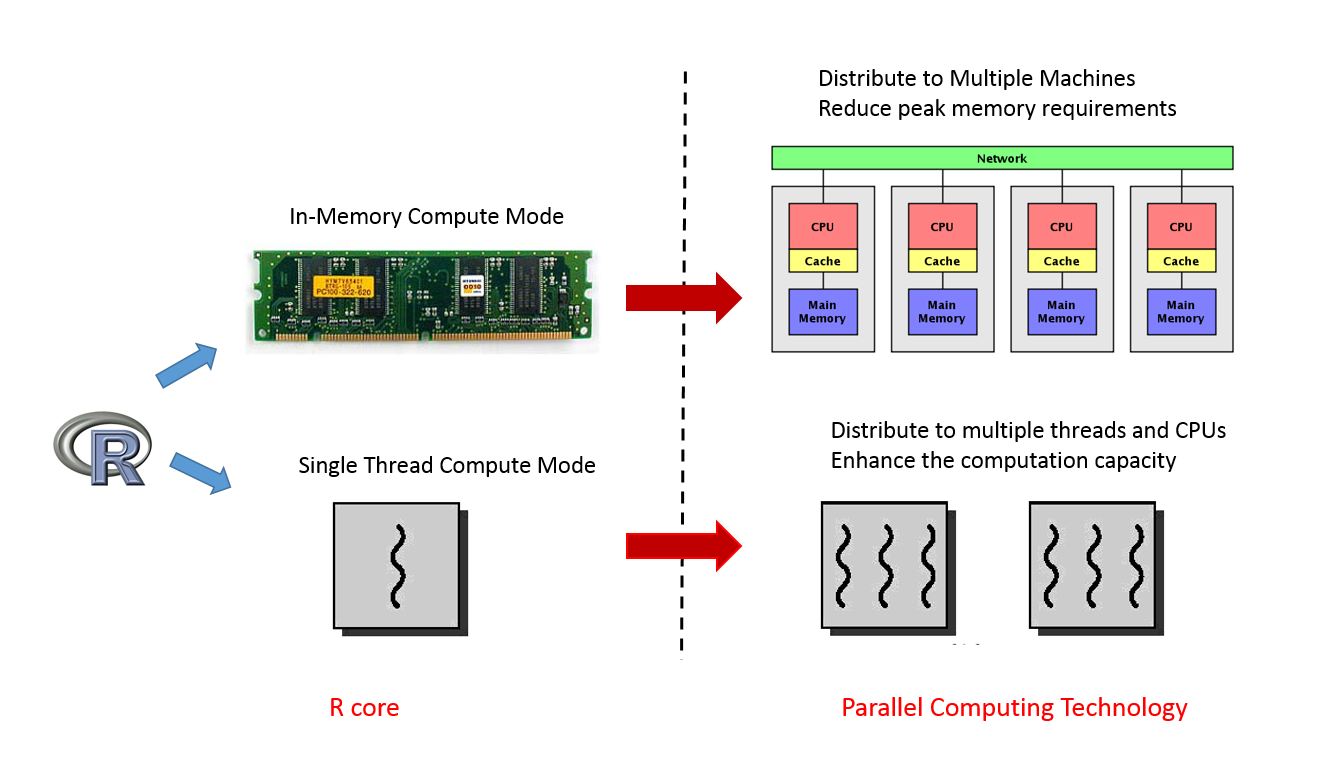
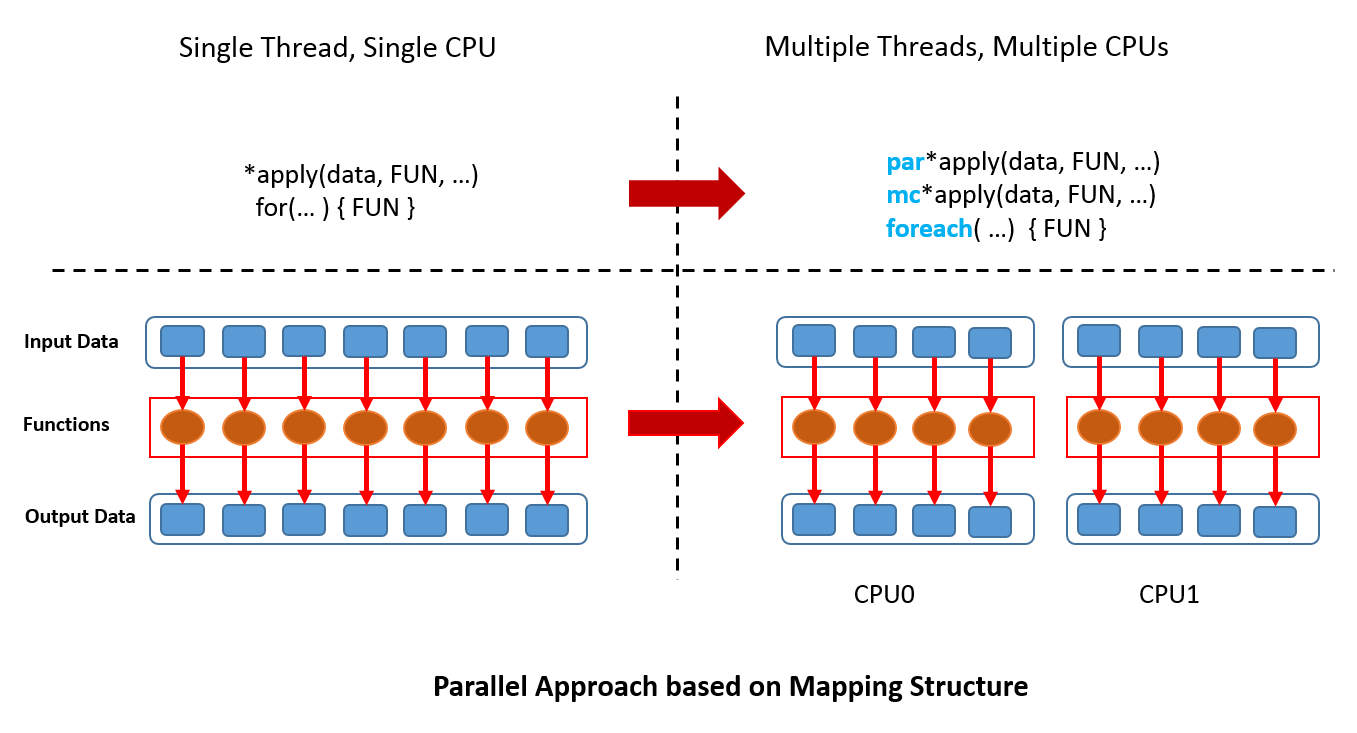
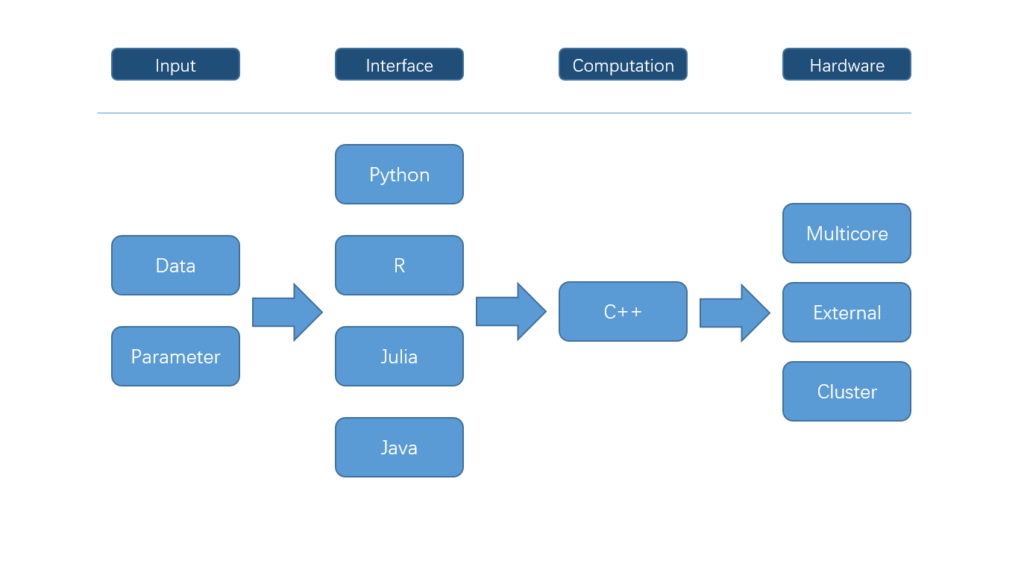 Although it is common that an R package is a wrapper of another tool, not many packages have the backend supporting many ways of parallel computation. In xgboost, most works are done in the C++ part in the above Figure. Since all interfaces share the same computational backend, there is not really a difference in terms of the accuracy or efficiency of the results from different interfaces. Users only need to prepare the data and parameters in the preferred language, then call the corresponding interface and wait for the training and prediction. This design puts most heavy works to the background, and only asks for the minimum support from each interface. For this reason, we can expect in the future there will be more languages wrapping the XGBoost backend and their users can enjoy the parallel training power. XGBoost implements a gradient boosting trees algorithm. A gradient boosting trees model trains a lot of decision trees or regression trees in a sequence, where only one tree is added to the model at a time, and every new tree depends on the previous trees. This nature limits the level of parallel computation, since we cannot build multiple trees simultaneously. Therefore, the parallel computation is introduced in a lower level, i.e. in the tree-building process at each step.
Although it is common that an R package is a wrapper of another tool, not many packages have the backend supporting many ways of parallel computation. In xgboost, most works are done in the C++ part in the above Figure. Since all interfaces share the same computational backend, there is not really a difference in terms of the accuracy or efficiency of the results from different interfaces. Users only need to prepare the data and parameters in the preferred language, then call the corresponding interface and wait for the training and prediction. This design puts most heavy works to the background, and only asks for the minimum support from each interface. For this reason, we can expect in the future there will be more languages wrapping the XGBoost backend and their users can enjoy the parallel training power. XGBoost implements a gradient boosting trees algorithm. A gradient boosting trees model trains a lot of decision trees or regression trees in a sequence, where only one tree is added to the model at a time, and every new tree depends on the previous trees. This nature limits the level of parallel computation, since we cannot build multiple trees simultaneously. Therefore, the parallel computation is introduced in a lower level, i.e. in the tree-building process at each step.  Specifically, the parallel computation takes place in the operation where the model scans through all features on each internal node and set a threshold. Say we have a 4-core CPU for the training computation, then XGBoost separate the features into 4 groups. For the splitting operation on a node, XGBoost distributes the operation on each feature to their corresponding core. The training data is stored in a piece of shared memory, each core only needs to access one group of features, and perform the computation individually. The implementation is done in C++ with the help of OpenMP. It is obvious that users can benefit fully from the parallel computation if the number of features is larger than the number of threads of the CPU. XGBoost also supports training on a cluster, or with external memory. We will briefly introduce them in the following parts.
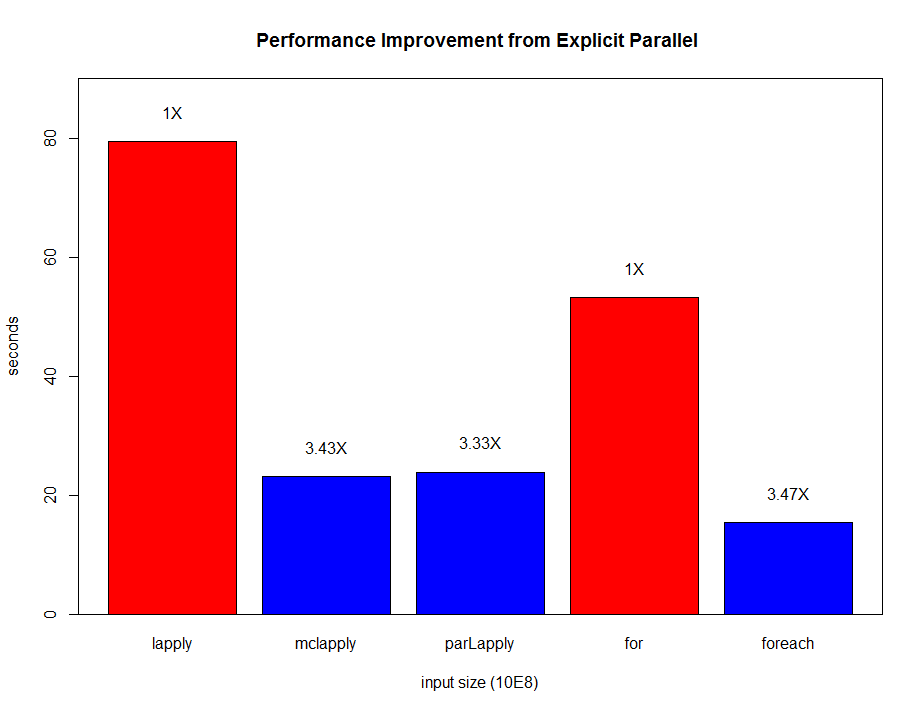
Specifically, the parallel computation takes place in the operation where the model scans through all features on each internal node and set a threshold. Say we have a 4-core CPU for the training computation, then XGBoost separate the features into 4 groups. For the splitting operation on a node, XGBoost distributes the operation on each feature to their corresponding core. The training data is stored in a piece of shared memory, each core only needs to access one group of features, and perform the computation individually. The implementation is done in C++ with the help of OpenMP. It is obvious that users can benefit fully from the parallel computation if the number of features is larger than the number of threads of the CPU. XGBoost also supports training on a cluster, or with external memory. We will briefly introduce them in the following parts.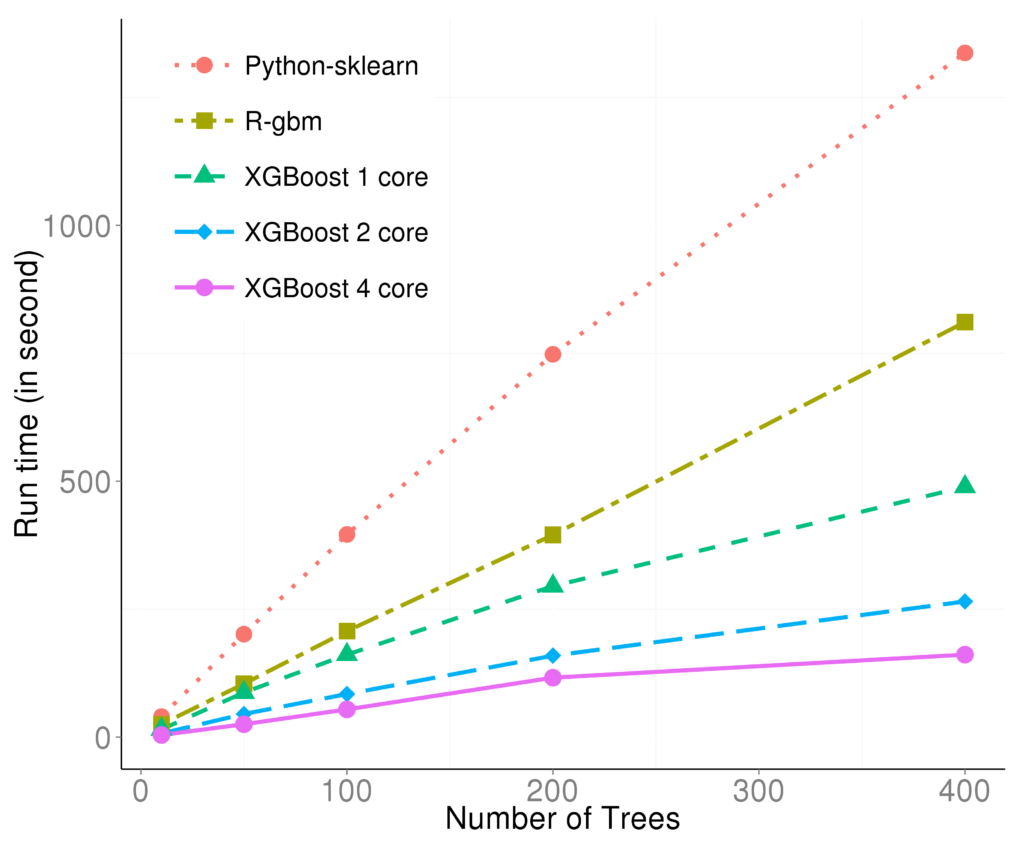 The marks R and python are the vanilla gradient boosting machine implementation. XGBoost is the fastest when using only one thread. By employing 4 threads the process can be almost 4x faster. To reproduce the above results, one can find related scripts at:
The marks R and python are the vanilla gradient boosting machine implementation. XGBoost is the fastest when using only one thread. By employing 4 threads the process can be almost 4x faster. To reproduce the above results, one can find related scripts at:

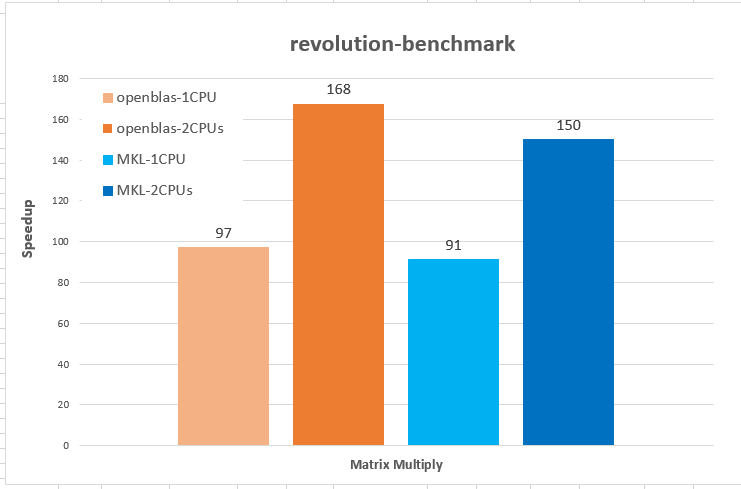
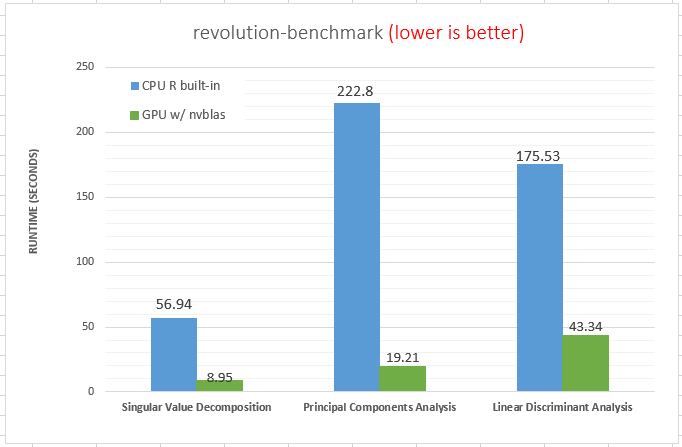
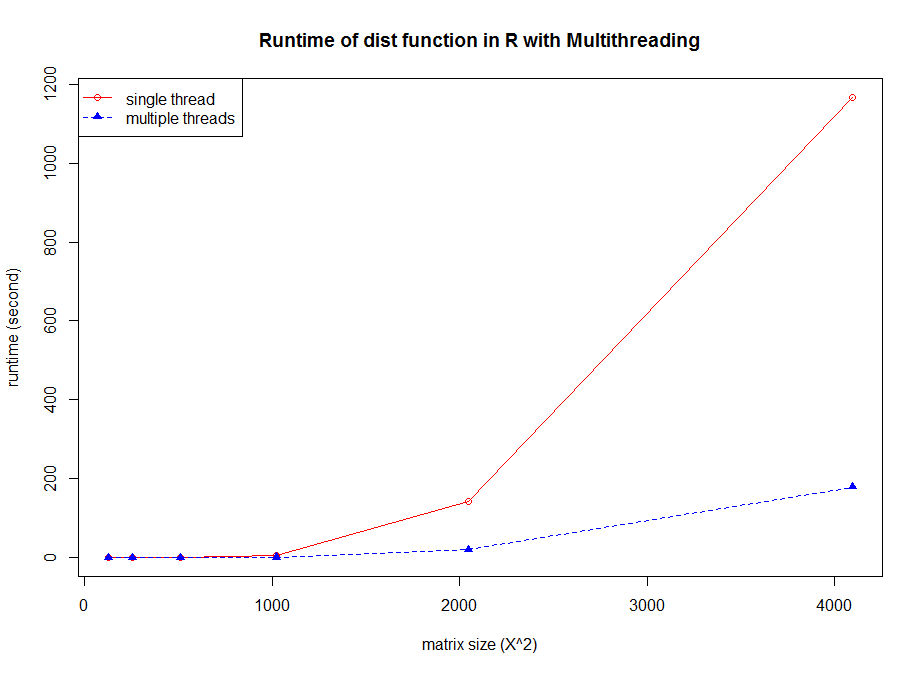
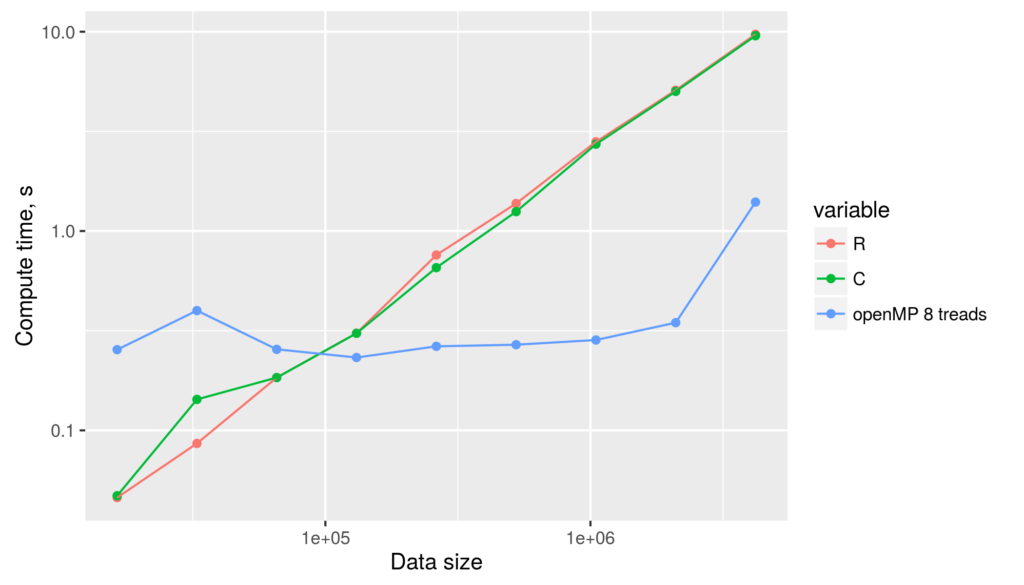 The figure reveals several facts. First, for non-parallelized code we can see that
The figure reveals several facts. First, for non-parallelized code we can see that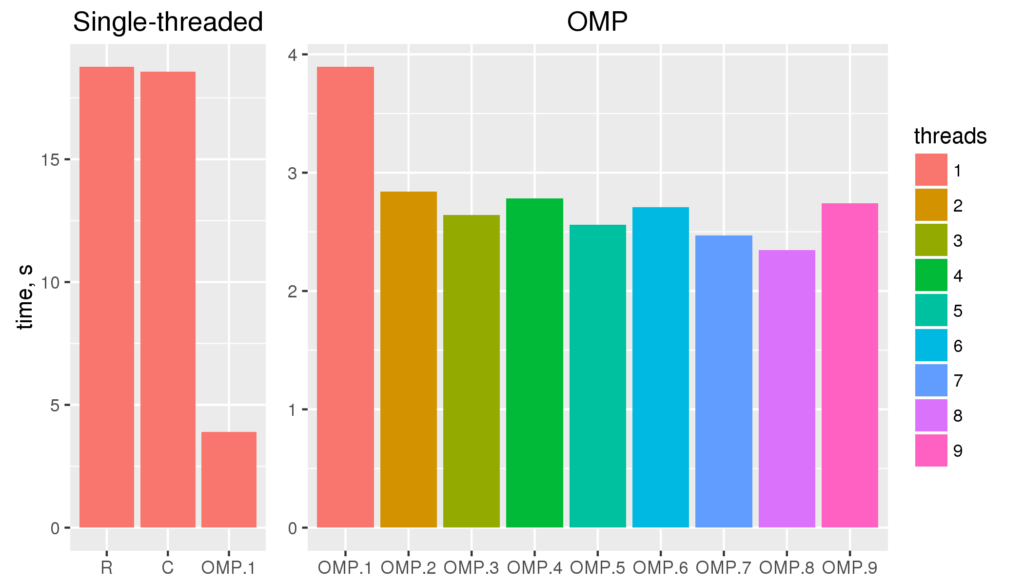 The figure shows the run time for single threaded versions of the code (R and C), and multi-threaded openMP versions with 1 to 9 threads (OMP.1 to OMP.9).
The figure shows the run time for single threaded versions of the code (R and C), and multi-threaded openMP versions with 1 to 9 threads (OMP.1 to OMP.9).

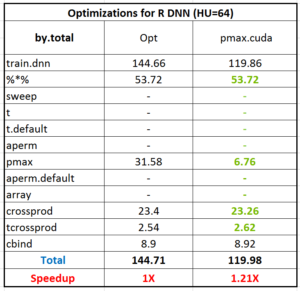
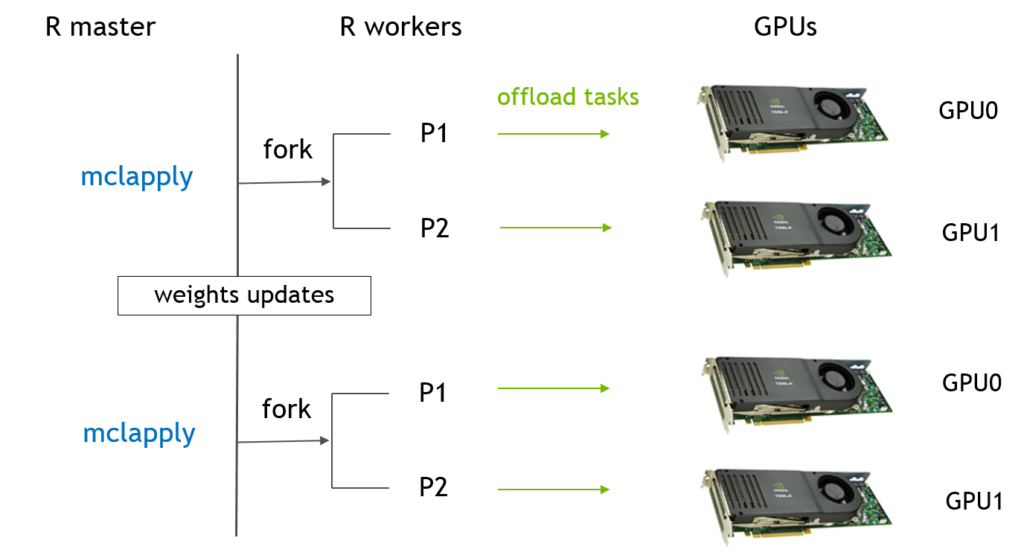
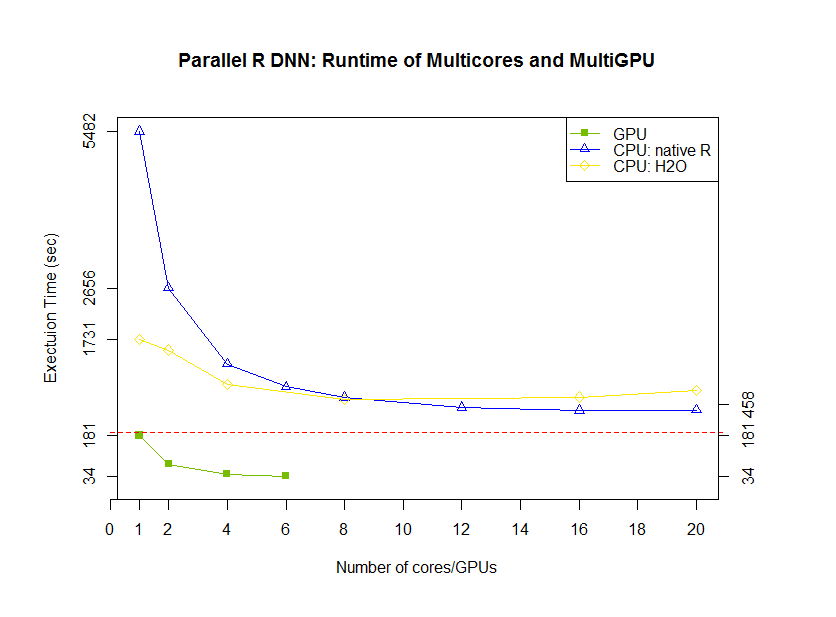
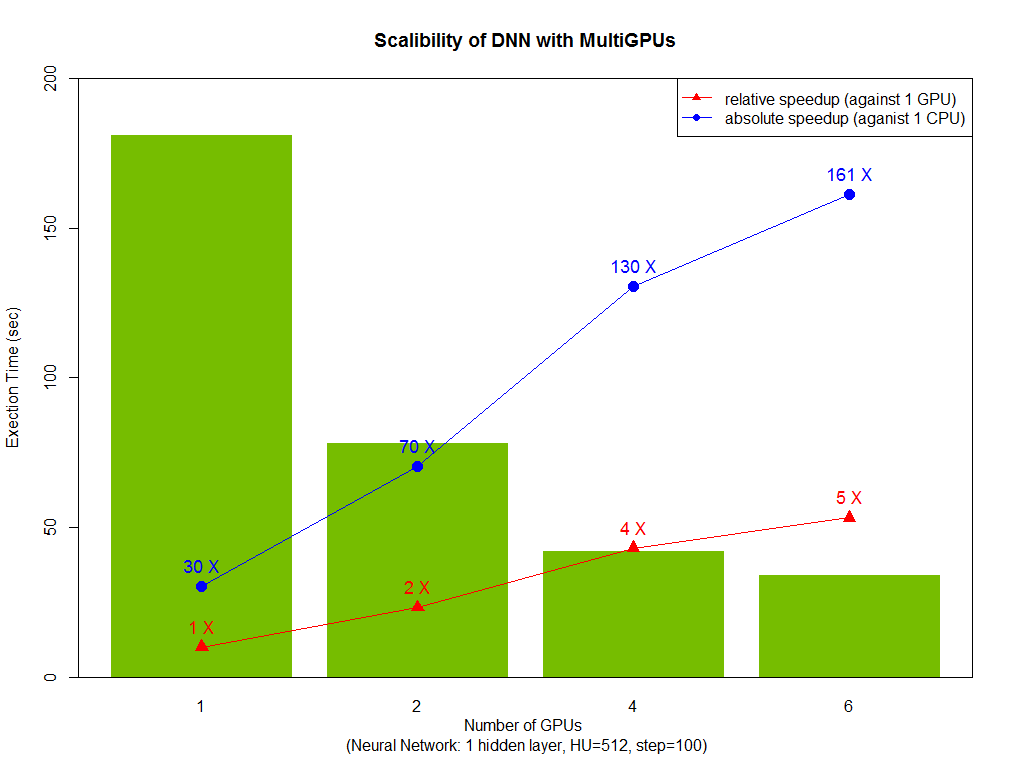
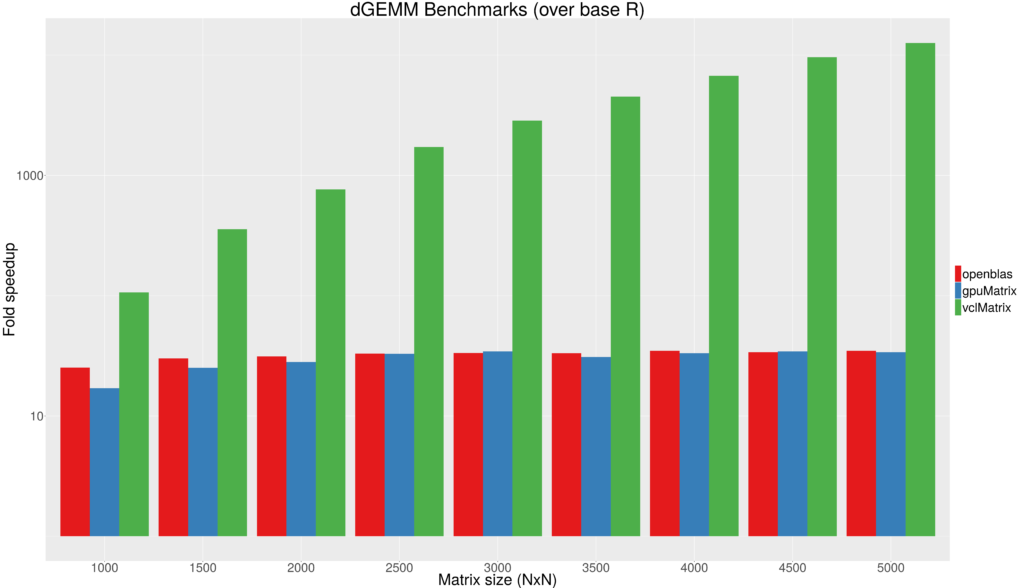 Figure 1 - Fold speedup achieved using openblas (CPU) as well as the gpuMatrix/vclMatrix (GPU) classes provided in gpuR.[/caption]
Figure 1 - Fold speedup achieved using openblas (CPU) as well as the gpuMatrix/vclMatrix (GPU) classes provided in gpuR.[/caption] 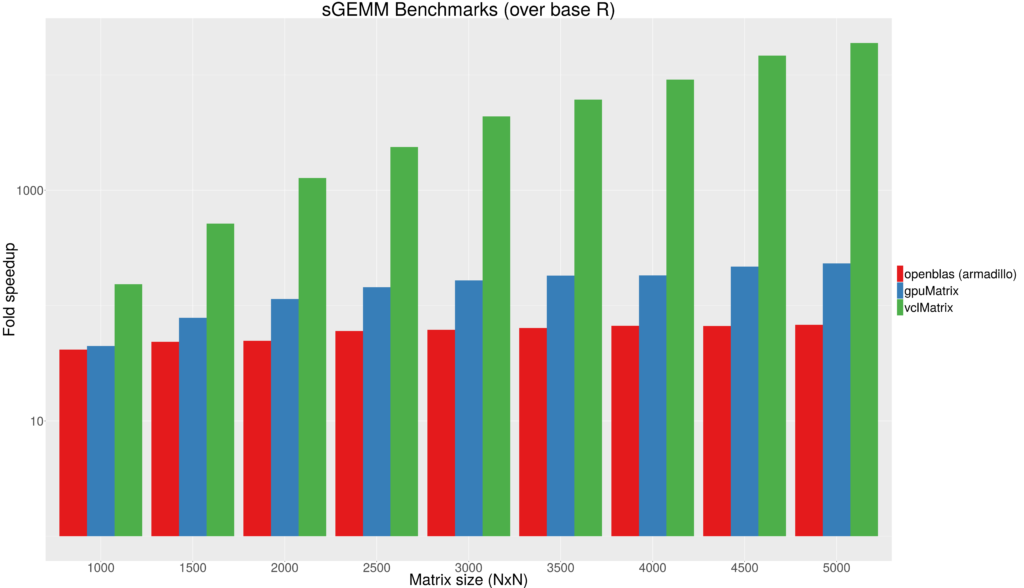 Figure 2 - Float type GEMM comparisons. Fold speedup achieved using openblas (via RcppArmadillo) as well as the gpuMatrix/vclMatrix (GPU) classes provided in gpuR.[/caption] To give an additional view on the performance achieved by
Figure 2 - Float type GEMM comparisons. Fold speedup achieved using openblas (via RcppArmadillo) as well as the gpuMatrix/vclMatrix (GPU) classes provided in gpuR.[/caption] To give an additional view on the performance achieved by 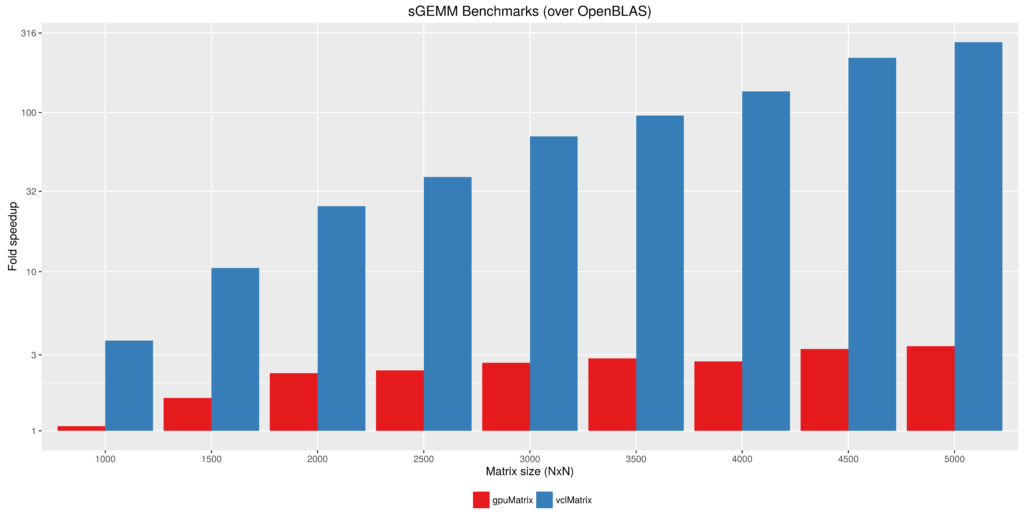 Figure 3 - Fold speedup achieved over openblas (via RcppArmadillo) float type GEMM comparisons vs the gpuMatrix/vclMatrix (GPU) classes provided in gpuR.[/caption]
Figure 3 - Fold speedup achieved over openblas (via RcppArmadillo) float type GEMM comparisons vs the gpuMatrix/vclMatrix (GPU) classes provided in gpuR.[/caption]